Wiskunde kan soms een uitdaging lijken, vooral als het gaat om het berekenen van de omtrek en oppervlakte van geometrische vormen. Twee veelvoorkomende vormen die je regelmatig zult tegenkomen zijn de cirkel en de driehoek. In dit artikel leggen we je stap voor stap uit hoe je de omtrek van een cirkel berekent, de oppervlakte van een cirkel, en ook de oppervlakte van een driehoek. We zullen de formules bespreken, voorbeelden geven en tips delen om de berekeningen gemakkelijk te maken.
Wat is Omtrek en Oppervlakte?
Voordat we dieper ingaan op de specifieke berekeningen, is het belangrijk om te begrijpen wat omtrek en oppervlakte precies betekenen:
- Omtrek is de totale afstand rond de rand van een figuur. Bij een cirkel is dit de lengte van de cirkel zelf, en bij een driehoek is dit de som van de lengtes van de drie zijden.
- Oppervlakte is de hoeveelheid ruimte die een vorm op een vlak inneemt. Dit wordt meestal uitgedrukt in vierkante eenheden (bijv. vierkante meters).
Nu we dat hebben uitgelegd, gaan we verder met de formules voor de omtrek en oppervlakte van de cirkel en driehoek.
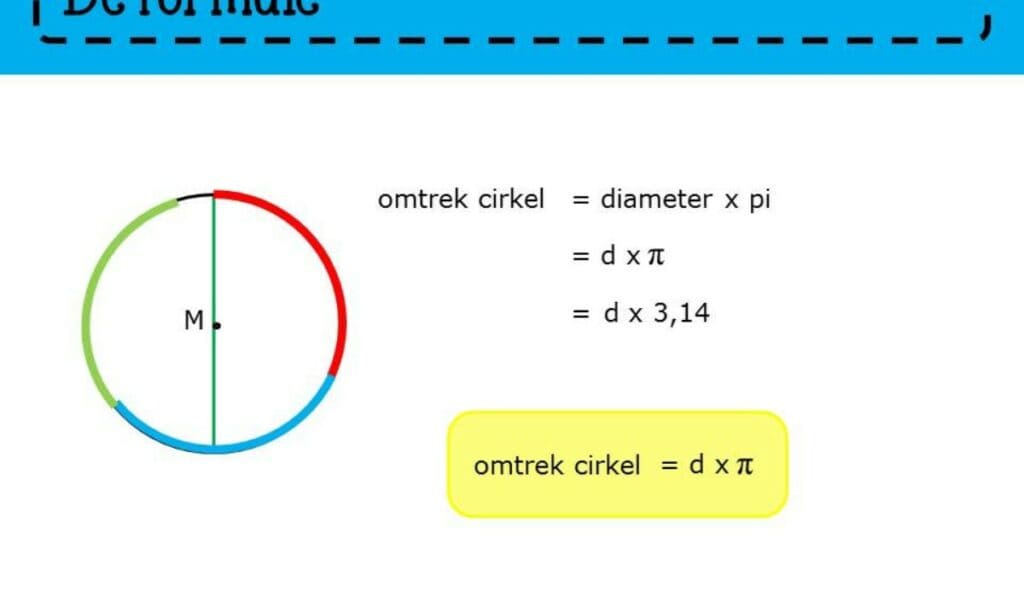
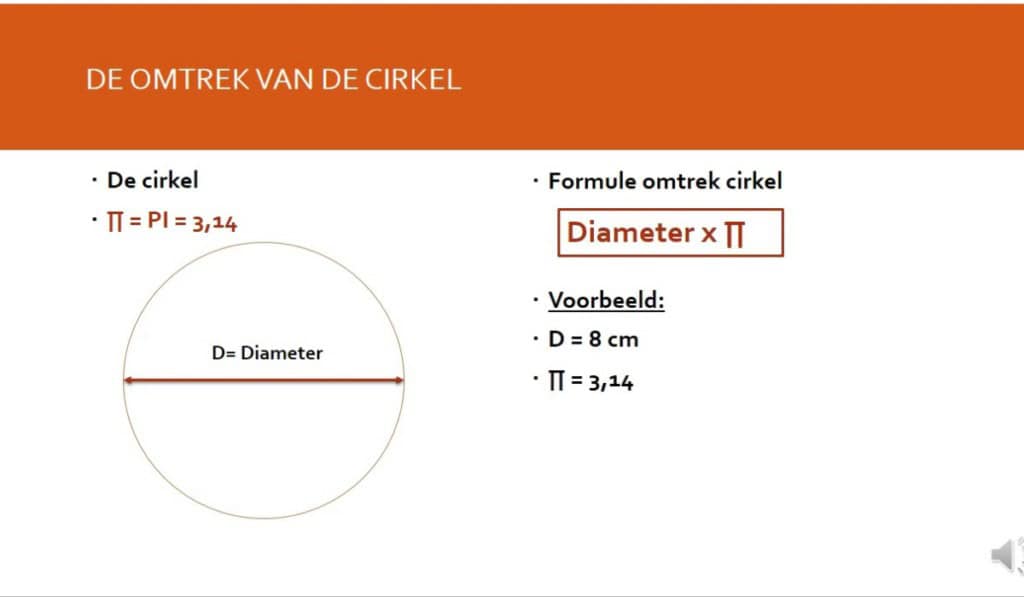
Omtrek Cirkel Berekenen
De formule om de omtrek van een cirkel te berekenen is vrij eenvoudig. De omtrek van een cirkel wordt berekend met de volgende formule:
O=2πrO = 2 \pi rO=2πr
Waarbij:
- O staat voor de omtrek.
- r de straal van de cirkel is.
- π (pi) is een wiskundige constante die ongeveer gelijk is aan 3,14159.
Voorbeeld:
Stel je voor dat de straal van een cirkel 5 cm is. De omtrek bereken je dan als volgt:
O=2×3,14159×5=31,4159 cmO = 2 \times 3,14159 \times 5 = 31,4159 \, \text{cm}O=2×3,14159×5=31,4159cm
Dus, de omtrek van deze cirkel is ongeveer 31,42 cm.
Oppervlakte Cirkel Berekenen
De oppervlakte van een cirkel wordt berekend met de volgende formule:
A=πr2A = \pi r^2A=πr2
Waarbij:
- A de oppervlakte is.
- r de straal van de cirkel is.
Voorbeeld:
Als de straal van de cirkel opnieuw 5 cm is, dan is de oppervlakte als volgt:
A=3,14159×(5)2=3,14159×25=78,53975 cm2A = 3,14159 \times (5)^2 = 3,14159 \times 25 = 78,53975 \, \text{cm}^2A=3,14159×(5)2=3,14159×25=78,53975cm2
De oppervlakte van de cirkel is dus ongeveer 78,54 cm².
Omtrek Driehoek Berekenen
De omtrek van een driehoek wordt berekend door de lengtes van de drie zijden bij elkaar op te tellen. Als we een driehoek hebben met zijden van a, b, en c, dan is de formule:
O=a+b+cO = a + b + cO=a+b+c
Voorbeeld:
Stel dat we een driehoek hebben met de volgende zijden: 6 cm, 8 cm, en 10 cm. De omtrek is dan:
O=6+8+10=24 cmO = 6 + 8 + 10 = 24 \, \text{cm}O=6+8+10=24cm
Dus de omtrek van deze driehoek is 24 cm.
Oppervlakte Driehoek Berekenen
De oppervlakte van een driehoek kan op verschillende manieren worden berekend, afhankelijk van de gegevens die we hebben. De meest voorkomende formule is de volgende, die gebruik maakt van de basis en de hoogte van de driehoek:
A=12×basis×hoogteA = \frac{1}{2} \times \text{basis} \times \text{hoogte}A=21×basis×hoogte
Voorbeeld:
Stel je voor dat we een driehoek hebben met een basis van 8 cm en een hoogte van 5 cm. De oppervlakte bereken je dan als volgt:
A=12×8×5=20 cm2A = \frac{1}{2} \times 8 \times 5 = 20 \, \text{cm}^2A=21×8×5=20cm2
Dus de oppervlakte van de driehoek is 20 cm².
Alternatieve Formule: Heron’s Formule
Als je de lengtes van de drie zijden van de driehoek hebt, maar geen hoogte, kun je de Heron’s formule gebruiken. Dit is handig wanneer je geen rechtopstaande hoogte hebt.
De formule voor Heron’s is als volgt:
A=s(s−a)(s−b)(s−c)A = \sqrt{s(s-a)(s-b)(s-c)}A=s(s−a)(s−b)(s−c)
Waarbij:
- a, b, en c de lengtes van de drie zijden zijn.
- s de halve omtrek is, dus s = \frac{a + b + c}{2}.
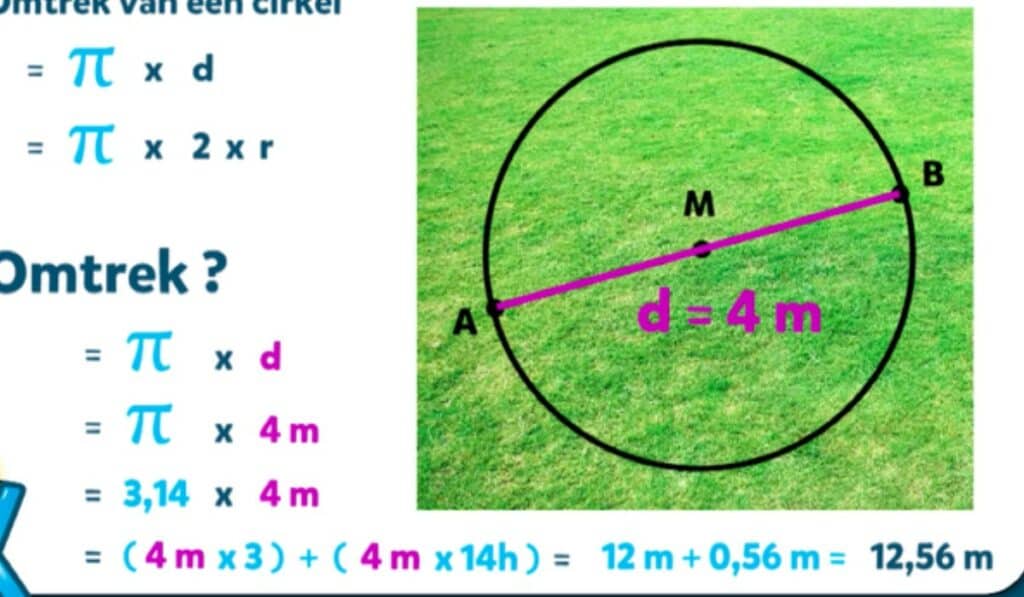
Omtrek van een Cirkel: Hoe Je Het Correct Berekent
Het berekenen van de omtrek en oppervlakte van een cirkel of driehoek is een essentiële vaardigheid in de wiskunde. Of je nu de omtrek van een cirkel moet berekenen, de oppervlakte van een driehoek wilt vinden, of gewoon meer wilt leren over geometrie, de formules en voorbeelden die we hebben besproken, zullen je helpen om deze concepten beter te begrijpen. Met een beetje oefening zal je in staat zijn om snel en nauwkeurig deze berekeningen uit te voeren.
